Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms. It is in terms of a Lie group  , to generalise the groups SL2(R) or PSL2 (R) of modular forms, and a discrete group
, to generalise the groups SL2(R) or PSL2 (R) of modular forms, and a discrete group 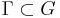 , to generalise the modular group, or one of its congruence subgroups.
, to generalise the modular group, or one of its congruence subgroups.
Contents |
Formulation
The formulation requires the general notion of factor of automorphy  for
for 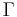 , which is a type of 1-cocycle in the language of group cohomology. The values of
, which is a type of 1-cocycle in the language of group cohomology. The values of  may be complex numbers, or in fact complex square matrices, corresponding to the possibility of vector-valued automorphic forms. The cocycle condition imposed on the factor of automorphy is something that can be routinely checked, when
may be complex numbers, or in fact complex square matrices, corresponding to the possibility of vector-valued automorphic forms. The cocycle condition imposed on the factor of automorphy is something that can be routinely checked, when  is derived from a Jacobian matrix, by means of the chain rule.
is derived from a Jacobian matrix, by means of the chain rule.
In the general setting, then, an automorphic form is a function  on
on  (with values in some fixed finite-dimensional vector space
(with values in some fixed finite-dimensional vector space  , in the vector-valued case), subject to three kinds of conditions:
, in the vector-valued case), subject to three kinds of conditions:
- to transform under translation by elements
 according to the given automorphy factor
according to the given automorphy factor  ;
; - to be an eigenfunction of certain Casimir operators on
 ; and
; and - to satisfy some conditions on growth at infinity.
It is the first of these that makes  automorphic, that is, satisfy an interesting functional equation relating
automorphic, that is, satisfy an interesting functional equation relating 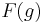 with
with 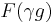 for
for  . In the vector-valued case the specification can involve a finite-dimensional group representation ρ acting on the components to 'twist' them. The Casimir operator condition says that some Laplacians have
. In the vector-valued case the specification can involve a finite-dimensional group representation ρ acting on the components to 'twist' them. The Casimir operator condition says that some Laplacians have  as eigenfunction; this ensures that
as eigenfunction; this ensures that  has excellent analytic properties, but whether it is actually a complex-analytic function depends on the particular case. The third condition is to handle the case where
has excellent analytic properties, but whether it is actually a complex-analytic function depends on the particular case. The third condition is to handle the case where 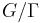 is not compact but has cusps.
is not compact but has cusps.
History
Before this very general setting was proposed (around 1960), there had already been substantial developments of automorphic forms other than modular forms. The case of 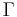 a Fuchsian group had already received attention before 1900 (see below). The Hilbert modular forms (Hilbert-Blumenthal, as one should say) were proposed not long after that, though a full theory was long in coming. The Siegel modular forms, for which
a Fuchsian group had already received attention before 1900 (see below). The Hilbert modular forms (Hilbert-Blumenthal, as one should say) were proposed not long after that, though a full theory was long in coming. The Siegel modular forms, for which  is a symplectic group, arose naturally from considering moduli spaces and theta functions. The post-war interest in several complex variables made it natural to pursue the idea of automorphic form in the cases where the forms are indeed complex-analytic. Much work was done, in particular by Ilya Piatetski-Shapiro, in the years around 1960, in creating such a theory. The theory of the Selberg trace formula, as applied by others, showed the considerable depth of the theory. Robert Langlands showed how (in generality, many particular cases being known) the Riemann-Roch theorem could be applied to the calculation of dimensions of automorphic forms; this is a kind of post hoc check on the validity of the notion. He also produced the general theory of Eisenstein series, which corresponds to what in spectral theory terms would be the 'continuous spectrum' for this problem, leaving the cusp form or discrete part to investigate. From the point of view of number theory, the cusp forms had been recognised, since Srinivasa Ramanujan, as the heart of the matter.
is a symplectic group, arose naturally from considering moduli spaces and theta functions. The post-war interest in several complex variables made it natural to pursue the idea of automorphic form in the cases where the forms are indeed complex-analytic. Much work was done, in particular by Ilya Piatetski-Shapiro, in the years around 1960, in creating such a theory. The theory of the Selberg trace formula, as applied by others, showed the considerable depth of the theory. Robert Langlands showed how (in generality, many particular cases being known) the Riemann-Roch theorem could be applied to the calculation of dimensions of automorphic forms; this is a kind of post hoc check on the validity of the notion. He also produced the general theory of Eisenstein series, which corresponds to what in spectral theory terms would be the 'continuous spectrum' for this problem, leaving the cusp form or discrete part to investigate. From the point of view of number theory, the cusp forms had been recognised, since Srinivasa Ramanujan, as the heart of the matter.
Automorphic representations
The subsequent notion of automorphic representation has proved of great technical value for dealing with  an algebraic group, treated as an adelic algebraic group. It does not completely include the automorphic form idea introduced above, in that the adele approach is a way of dealing with the whole family of congruence subgroups at once. Inside an
an algebraic group, treated as an adelic algebraic group. It does not completely include the automorphic form idea introduced above, in that the adele approach is a way of dealing with the whole family of congruence subgroups at once. Inside an 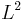 space for a quotient of the adelic form of
space for a quotient of the adelic form of  , an automorphic representation is a representation that is an infinite tensor product of representations of p-adic groups, with specific enveloping algebra representations for the infinite prime(s). One way to express the shift in emphasis is that the Hecke operators are here in effect put on the same level as the Casimir operators; which is natural from the point of view of functional analysis, though not so obviously for the number theory. It is this concept that is basic to the formulation of the Langlands philosophy.
, an automorphic representation is a representation that is an infinite tensor product of representations of p-adic groups, with specific enveloping algebra representations for the infinite prime(s). One way to express the shift in emphasis is that the Hecke operators are here in effect put on the same level as the Casimir operators; which is natural from the point of view of functional analysis, though not so obviously for the number theory. It is this concept that is basic to the formulation of the Langlands philosophy.
Poincaré on psychology of discovery and his work on automorphic functions
Poincaré's first area of interest in mathematics, dating to the 1880s, was automorphic forms. He named them Fuchsian functions, after the mathematician Lazarus Fuchs, because Fuchs was known for being a good teacher and had researched on differential equations and the theory of functions. Poincaré actually developed the concept of these functions as part of his doctoral thesis. Under Poincaré's definition, an automorphic function is one which is analytic in its domain and is invariant under a denumerable infinite group of linear fractional transformations. Automorphic functions then generalize both trigonometric and elliptic functions.
Poincaré explains how he discovered Fuchsian functions:
- For fifteen days I strove to prove that there could not be any functions like those I have since called Fuchsian functions. I was then very ignorant; every day I seated myself at my work table, stayed an hour or two, tried a great number of combinations and reached no results. One evening, contrary to my custom, I drank black coffee and could not sleep. Ideas rose in crowds; I felt them collide until pairs interlocked, so to speak, making a stable combination. By the next morning I had established the existence of a class of Fuchsian functions, those which come from the hypergeometric series; I had only to write out the results, which took but a few hours.
See also
References
- A.N. Parshin (2001), "Automorphic Form", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=a/a014160
- Henryk Iwaniec, Spectral Methods of Automorphic Forms, Second Edition, (2002) (Volume 53 in Graduate Studies in Mathematics), American Mathematical Society, Providence, RI ISBN 0-8218-3160-7
This article incorporates material from Jules Henri Poincaré on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.